The Function Ontology

Unofficial Draft

More details about this document
Latest published version:
none
Latest editor's draft:
https://w3id.org/function/spec/
Editors:
Ben De Meester (Ghent University – imec – IDLab)
(Ghent University – imec – IDLab)
Authors:
Ben De Meester (Ghent University – imec – IDLab)
(Ghent University – imec – IDLab)
(Research Studios Austria Forschungsgesellschaft mbH – Studio SAT)
This Version
https://w3id.org/function/spec/20230512/
Previous Version
https://w3id.org/function/spec/20211110/
Website
https://fno.io

Copyright © 2016-2023 the document editors/authors. Text is available under the Creative Commons Attribution 4.0 International Public License; additional terms may apply.

Abstract

This document discusses the Function Ontology: a way to semantically declare and describe implementation-independent functions, and their relations to related concepts such as parameters, outputs, related problems, algorithms, mappings to concrete implementations, and executions.

A list of the publications concerning the Function Ontology can be viewed at https://fno.io.

The main scientific publication is Implementation-independent function reuse [10.1016/j.future.2019.10.006].

Namespace

The Function Ontology's namespace is https://w3id.org/function/ontology#

The preferred prefix is fno:

The discussed ontology's version is 1.0.0.

The used vocabularies are

Status of This Document

This document is a draft of a potential specification. It has no official standing of any kind and does not represent the support or consensus of any standards organization.

This is an early draft, yet efforts are made to keep things stable, given the uptake of FnO in, among others, RML.io.

1. Conformance

As well as sections marked as non-normative, all authoring guidelines, diagrams, examples, and notes in this specification are non-normative. Everything else in this specification is normative.

The key words MUST and SHOULD in this document are to be interpreted as described in BCP 14 [RFC2119] [RFC8174] when, and only when, they appear in all capitals, as shown here.

2. The Problem

Functions are processes that perform a specific task by associating one or more inputs to an output. They are essential building blocks of information retrieval and information management, and of computer science in general. For example, during extraction of birthdates from a semi-structured dataset, normalization of these dates improves further analysis.

However, the development, maintenance, and support efforts of implementing these functions are fragmented. Efforts are fragmented across different development contexts (i.e., a combination of, among others, programming language, programming paradigm, and architecture), and it is not feasible to consolidate these efforts by limiting all developers to the same development context. On the one hand because implementations are tuned to meet different requirements, on the other hand due to prior investment. Thus, the same function can have multiple implementations, each within a specific development context. For example, a function to normalize dates may have implementations available as a piece of JavaScript source code, as part of a JAVA software package, and within a RESTful Web service.

This specification (and accompanying ontology) explains how to semantically declare and describe functions, their input parameters, and possible outputs. Instead of defining technology-specifics, the functions are described independent of the technology that implements them. By semantically defining these functions using an ontology, we provide a uniform and unambiguous solution, and thus, we can close the gap between semantic data and any real-world action, and enable semantic applications to be used in real-world scenarios.

We furthermore provide links to other – not further specified – concepts such as problems and algorithms, and specify the additional mappings of these abstract functions to (existing) concrete implementations.

3. Definitions

The following document makes a clear distinction between following concepts:

Furthermore, we define following concepts:

In this specification, a problem and algorithm are not described in further detail. We mostly provide generic relations to point to other vocabularies or ontologies. This way, problems and algorithms can be further specified in complementary vocabularies.

4. The Function Ontology

The Function Ontology distinguishes between the (abstract) function and the (concrete) implementation. The two can be used together, but are complementary.

4.1 Function (abstract)

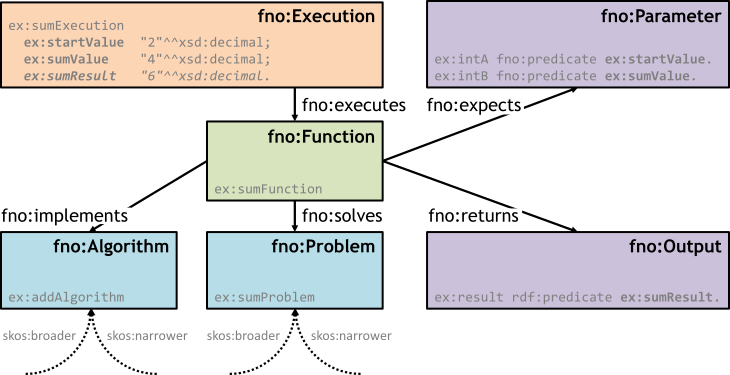
The Function Ontology
Figure 1 The Function Ontology

The Function Ontology follows the Content Ontology Design Pattern and consists of a couple of base classes that need to be instantiated for real world use cases. Input parameters and output values are connected to functions via executions, using a reification paradigm [rdf-primer].

It uses SKOS to define relations between functions, problems, and algorithms [skos-primer].

To be consistent with the paradigms used in SKOS, axioms need to be made instead of subclassing the base classes of the Function Ontology. The reification paradigm allows to define the connection between an execution and the input parameters and output values. This allows for reusing these connection definitions, and more meaningful connections between input parameters and execution.

No cardinalities are defined in the Function Ontology, as there are no hard limits on cardinality to be defined. A function can implement multiple algorithms, solve multiple problems, and have multiple executions. All executions can have multiple input parameters and output values. Vice versa, input parameters and output values can be linked to multiple executions, and an execution (i.e., a set of input values and output values) can be linked to multiple functions.

4.1.1 fno:Function

Example 1: 
ex:sumFunction
    a                   fno:Function ;
    fno:name            "The sum function"^^xsd:string ;
    dcterms:description "This function can do the sum of two integers."^^xsd:string .

This is a function declaration: a sum function is defined and described.

4.1.2 fno:Problem

Example 2: 
ex:sumFunction
    a          fno:Function ;
    fno:solves ex:sumProblem .

ex:sumProblem
    a                   fno:Problem ;
    fno:name            "The sum problem"^^xsd:string ;
    dcterms:description "This handles the problem of adding two integers to each other."^^xsd:string ;
    skos:broader        ex:mathProblem .

Functions can be linked to Problems, which are more general descriptions than functions, e.g., the “Euclidean distance”-function is related to the “Distance”-problem. To create a more specific organization, problems can be further interlinked with each other using the SKOS standard [skos-primer].

Note

skos terms can be used to relate problems with each other. This can also be done for algorithms and functions.

4.1.2.1 fno:solves

Domain fno:Function

Range fno:Problem

4.1.3 fno:Algorithm

Example 3: 
ex:sumFunction
    a              fno:Function ;
    fno:implements ex:sumAlgorithm .

ex:sumAlgorithm
    a                   fno:Algorithm ;
    fno:name            "The sum algorithm"^^xsd:string ;
    dcterms:description "About how to add two integers to each other."^^xsd:string ;
4.1.3.1 fno:implements

Domain fno:Function

Range fno:Algorithm

4.1.4 fno:Parameter

Example 4: 
ex:sumFunction
    a           fno:Function ;
    fno:expects ( ex:intParameterA ex:intParameterB ) .

ex:intParameterA
    a             fno:Parameter ;
    fno:predicate ex:startValue ;
    fno:type      xsd:integer ;
    fno:required  "true"^^xsd:boolean .

ex:intParameterB
    a             fno:Parameter ;
    fno:predicate ex:sumValue ;
    fno:type      xsd:integer ;
    fno:required  "true"^^xsd:boolean .

A Function expects a list of Parameters and returns a list of Outputs. This description actually defines which predicates to use when binding the values to the execution of the function. The parameters are ordered in a list, and each parameter defines the relationship that is used for the execution. For this, the fno:predicate predicate MUST be used. All predicates are allowed, except for rdf:type and fno:executes. A Parameter can have a specific type or other metadata (e.g., required or not, having a default value or not).

To specify the datatype of the parameter, the fno:type predicate SHOULD be used.

To specify whether a parameter is required, the fno:required predicate SHOULD be used.

In the example ex:intParameterA and ex:intParameterB can be reused across function descriptions. As they only describe the parameters, and not the actual values, they can be reused. For example, the function function match(str, regex) and function split(str, regex) could reuse the same parameter instantiations.

The fno:expects predicate has as range rdf:List. This could be used to hint applications how many parameters are used, and in what order, however, this is not enforced. This to accommodate technologies where the order of parameters is not important.

4.1.4.1 fno:expects

Domain fno:Function

Range rdf:List of fno:Parameter

4.1.4.2 fno:predicate

Domain fno:Parameter | fno:Output

Range rdf:Property

4.1.4.3 fno:type

Domain fno:Parameter | fno:Output

4.1.4.4 fno:required

Domain fno:Parameter | fno:Output

Range xsd:boolean

4.1.5 fno:Execution

Example 5: 
ex:sumExecution
    a             fno:Execution ;
    fno:executes  ex:sumFunction ;
    ex:startValue "2"^^xsd:integer ;
    ex:sumValue   "4"^^xsd:integer.

The Execution shows how the predicates are used as described as Parameters of the Function. rdf:type and fno:executes cannot be used as parameter predicates, as this would conflict with the description of the execution.

4.1.5.1 fno:executes

Domain fno:Execution

Range fno:Function

4.1.6 fno:Output

Example 6: 
ex:sumFunction
    a           fno:Function ;
    fno:returns ( ex:sumOutput ) .

ex:sumOutput
    a             fno:Output ;
    fno:predicate ex:sumResult ;
    fno:type      xsd:integer ;
    fno:required  "true"^^xsd:boolean .

A function's output is also a list, as multiple values can be returned (e.g., a Web API can return a body and a status code, a local implementation can return a value or throw an error). Similar as with fno:Parameter, the connecting predicate is described for fno:Output. To specify the datatype of the output, similarly, the fno:type predicate SHOULD be used.

After the execution of the function with the correct parameter values, we could return the following turtle:

Example 7: 
ex:sumExecution
    a            fno:Execution ;
    ex:sumResult "6"^^xsd:integer.

Similarly as with the parameter descriptions, the output descriptions can be reused across functions.

4.1.6.1 fno:returns

Domain fno:Function

Range rdf:List of fno:Output

4.1.7 Complete example

Declaration and description of the function and one execution:

Example 8: 
ex:sumFunction
    a                   fno:Function ;
    fno:name            "The sum function"^^xsd:string ;
    dcterms:description "This function can do the sum of two integers."^^xsd:string ;
    fno:solves          ex:sumProblem ;
    fno:implements      ex:sumAlgorithm ;
    fno:expects         ( ex: intParameterA ex:intParameterB ) ;
    fno:returns         ( ex:sumOutput ) .

ex:intParameterA
    a             fno:Parameter ;
    fno:predicate ex:startValue ;
    fno:type      xsd:integer ;
    fno:required  "true"^^xsd:boolean .

ex:intParameterB
    a             fno:Parameter ;
    fno:predicate ex:sumValue ;
    fno:type      xsd:integer ;
    fno:required  "true"^^xsd:boolean .

ex:sumOutput
    a             fno:Output ;
    fno:predicate ex:sumResult ;
    fno:type      xsd:integer ;
    fno:required  "true"^^xsd:boolean .

ex:sumProblem
    a                   fno:Problem ;
    fno:name            "The sum problem"^^xsd:string ;
    dcterms:description "This handles the problem of adding two integers to each other."^^xsd:string ;
    skos:broader        ex:mathProblem .

ex:sumAlgorithm
    a                   fno:Algorithm ;
    fno:name            "The sum algorithm"^^xsd:string ;
    dcterms:description "About how to add two integers to each other."^^xsd:string .

ex:sumExecution
    a             fno:Execution ;
    fno:executes  ex:sumFunction ;
    ex:startValue "2"^^xsd:integer ;
    ex:sumValue   "4"^^xsd:integer .

Resulting output triples:

Example 9: 
ex:sumExecution
    a            fno:Execution ;
    ex:sumResult "6"^^xsd:integer .

4.2 Implementation (concrete)

The Function Ontology
Figure 2 The Function Ontology, linked to implementations

4.2.1 fno:Implementation

Example 10: 
ex:leftPadImplementation
    a         fnoi:NpmPackage ;
    doap:name "left-pad" .
4.2.1.1 Example: Hydra

Link with the Hydra specification.

The Hydra specification defines Web services semantically. A hydra:ApiDocumentation can thus be seen as a specific fno:Implementation.

4.2.2 fno:Mapping

A fno:Mapping maps a fno:Function to a (part) of an fno:Implementation. For example: a left-pad function is mapped to a specific method in an NPM package. This requires the combination of 3 types of mappings:

  • the mapping of the method name (so that, e.g., a ex:leftPad function is mapped to method doLeftPadding()),
  • the mapping of the parameters (so that, e.g., the argument with predicate ex:inputString of the function is mapped to the second parameter of the doLeftPadding() method), and
  • the mapping of the outputs (so that, e.g., both the return value and the thrown exception of the method are mapped to the outputs of the function).

To link to the function and implementation, predicates fno:function and fno:implementation are used, respectively.

Note that the actual implementations and mappings are not part of the Function Ontology. Specific development contexts can be further catered to.

Example 11: 
ex:leftPadMapping
    a                  fno:Mapping ;
    fno:function       ex:leftPad ;
    fno:implementation ex:leftPadImplementation .
4.2.2.1 fno:MethodMapping

Maps the method name. For source code, this can be done using a fnom:StringMethodMapping. The method name is an attribute of a fnom:StringMethodMapping, linked using the fnom:method-name predicate.

Example 12: 
ex:leftPadMapping
    a                 fno:Mapping ;
    fno:methodMapping [ a                fnom:StringMethodMapping ;
                        fnom:method-name "doLeftPadding" ] .
4.2.2.2 fno:ParameterMapping

Maps the different parameters. For source code, this is typically specified by the position, using fnom:PositionParameterMapping: each fno:ParameterMapping gets linked to a parameter using the fnom:functionParameter predicate, and to a position using the fnom:implementationParameterPosition predicate.

Example 13: 
ex:leftPadMapping
    a                    fno:Mapping ;
    fno:parameterMapping [ a                                    fnom:PositionParameterMapping ;
                           fnom:functionParameter               ex:inputStringParameter ;
                           fnom:implementationParameterPosition "2"^^xsd:int ] .

For a Web service, this is typically specified by a name, e.g., a POST using property "password" in the form body. A fnom:PropertyParameterMapping is used. Each fno:ParameterMapping gets linked to a parameter using the fnom:functionParameter predicate, and to a property using the fnom:implementationProperty predicate.

4.2.2.3 fno:ReturnMapping

Maps the different outputs. For source code, this is typically specified by the return value, and (optionally) thrown exceptions, using fnom:DefaultReturnMapping and fnom:ExceptionReturnMapping, respectively: each fno:ReturnMapping gets linked to an output using the fnom:functionOutput predicate.

Example 14: 
ex:leftPadMapping
    a                 fno:Mapping ;
    fno:returnMapping [ a                   fnom:DefaultReturnMapping ;
                        fnom:functionOutput ex:outputStringOutput ] .

4.2.3 Execution with a Mapping

4.2.3.1 fno:uses

The metadata of the mapping can be linked to the execution using the fno:uses predicate

Example 15: 
ex:leftPadExecution
    fno:uses ex:leftPadMapping

4.2.4 Full example

Example 16: 
ex:leftPad
    a           fno:Function ;
    fno:expects ( ex:inputStringParameter ex:paddingParameter ) ;
    fno:returns ( ex:outputStringOutput ) .

ex:inputStringParameter
    a             fno:Parameter ;
    fno:predicate ex:inputString ;
    fno:type      xsd:string ;
    fno:required  "true"^^xsd:boolean .

ex:paddingParameter
    a             fno:Parameter ;
    fno:predicate ex:padding ;
    fno:type      xsd:int ;
    fno:required  "false"^^xsd:boolean .

ex:leftPadImplementation
    a         fnoi:NpmPackage ;
    doap:name "left-pad" .

ex:leftPadMapping
    a                    fno:Mapping ;
    fno:function         ex:leftPad ;
    fno:implementation   ex:leftPadImplementation ;
    fno:methodMapping    [ a                fnom:StringMethodMapping ;
                           fnom:method-name "doLeftPadding" ] ;
    fno:parameterMapping [ a                                    fnom:PositionParameterMapping ;
                           fnom:functionParameter               ex:inputStringParameter ;
                           fnom:implementationParameterPosition "2"^^xsd:int ] ;
    fno:parameterMapping [ a                                    fnom:PositionParameterMapping ;
                           fnom:functionParameter               ex:paddingParameter ;
                           fnom:implementationParameterPosition "1"^^xsd:int ] ;
    fno:returnMapping    [ a                   fnom:DefaultReturnMapping ;
                           fnom:functionOutput ex:outputStringOutput ] .

4.3 Function Composition

Function Composition is experimental and subject to change.

As an alternative to providing an implementation of a function, we can also define how it can be realized using other functions, namely by defining a composition. To illustrate this point, we first define a function, ex:sum3Function, that computes the sum of three integers. We are using the parameter and output definitions made earlier, so we only have to provide the third parameter, ex:intParameterC. For brevity, we omit the corresponding problem and algorithm.

Example 17: 
ex:sum3Function
    a                   fno:Function ;
    fno:name            "Sum3"^^xsd:string ;
    dcterms:description "This function calculates the sum of three integers."^^xsd:string ;
    fno:expects ( ex:intParameterA ex:intParameterB ex:intParameterC ) ;
    fno:returns ( ex:sumOutput ) 

ex:intParameterC
    a             fno:Parameter ;
    fno:predicate ex:sumValue2 ;
    fno:type      xsd:integer ;
    fno:required  "true"^^xsd:boolean .

4.3.1 fnoc:Composition

We will realize ex:sum3Function (defined in the previous paragraph) using ex:sumFunction introduced earlier, as illustrated with the following pseudo code: 

    ex:sum3Function(intParameterA, intParameterB, intParameterC) =  
        ex:sumFunction(ex:sumFunction(intParameterA, intParameterB), intParameterC)

In this construct, we use ex:sumFunction twice. In order to be able to reference the two distinct calls of the function ex:sumFunction unambiguously, we first create two distinct applications of it using fnoc:applies (This is only required when using the same function more than once in a composition). Then, we define the composition using a set of composition mappings.

Example 18: 

# create distinct instances of the function so we can reference them unambiguously 
ex:sum3Function_1 fnoc:applies ex:sumFunction .
ex:sum3Function_2 fnoc:applies ex:sumFunction .

# connect the parameters and outputs of ex:sum3Function, ex:sum3Function_1 and ex:sum3Function_2 
# to match our desired composition
ex:sum3Composition 
    a fnoc:Composition ;   
    fnoc:composedOf [
        fnoc:mapFrom [
            fnoc:constituentFunction ex:sum3Function;
            fnoc:functionParameter ex:intParameterA 
        ] ;
        fnoc:mapTo [
            fnoc:constituentFunction ex:sum3Function_1;
            fnoc:functionParameter ex:intParameterA
        ] 
    ],
    [
        fnoc:mapFrom [
            fnoc:constituentFunction ex:sum3Function;
            fnoc:functionParameter ex:intParameterB 
        ] ;
        fnoc:mapTo [
            fnoc:constituentFunction ex:sum3Function_1;
            fnoc:functionParameter ex:intParameterB
        ] 
    ],
    [
        fnoc:mapFrom [
            fnoc:constituentFunction ex:sum3Function_1;
            fnoc:functionOutput ex:sumOutput 
        ] ;
        fnoc:mapTo [
            fnoc:constituentFunction ex:sum3Function_2;
            fnoc:functionParameter ex:intParameterA
        ] 
    ],
    [
        fnoc:mapFrom [
            fnoc:constituentFunction ex:sum3Function;
            fnoc:functionParameter ex:intParameterC  
        ] ;
        fnoc:mapTo [
            fnoc:constituentFunction ex:sum3Function_2;
            fnoc:functionParameter ex:intParameterB
        ] 
    ],
    [
        fnoc:mapFrom [
            fnoc:constituentFunction ex:sum3Function_2;
            fnoc:functionOutput ex:sumOutput  
        ] ;
        fnoc:mapTo [
            fnoc:constituentFunction ex:sum3Function;
            fnoc:functionOutput ex:sumOutput
        ] 
    ] .

4.3.2 fnoc:CompositionMapping

Connects one function's parameter or output to another function's parameter or output. The properties used for this are mapFrom and mapTo . Alternatively, a CompositionMapping can link to a constant term via mapFromTerm instead of mapFrom.

4.3.3 fnoc:CompositionMappingEndpoint

The source or target of a compositionMapping, defining a combination of function and either parameter or output that is mapped to the target.

4.3.3.1 fnoc:composedOf

Domain fnoc:Composition

Range fnoc:CompositionMapping

4.3.3.2 fnoc:applies

Domain fno:Function

Range fno:Function

4.3.3.3 fnoc:constituentFunction

Domain fnoc:CompositionMappingEndpoint

Range fno:Function

4.3.3.4 fnoc:functionOutput

Domain fnoc:CompositionMappingEndpoint

Range fno:Output

4.3.3.5 fnoc:functionParameter

Domain fnoc:CompositionMappingEndpoint

Range fno:Parameter

4.3.3.6 fnoc:mapFrom

Domain fnoc:CompositionMapping

Range fnoc:CompositionMappingEndpoint

4.3.3.7 fnoc:mapFromTerm

Domain fnoc:CompositionMapping

Range (any)

Allows for using constants in a composition.

4.3.3.8 fnoc:mapTo

Domain fnoc:CompositionMapping

Range fnoc:CompositionMappingEndpoint

4.4 Partial Function Application

In the following example, we define the function ex:add10 as a partial application of ex:sumFunction by providing the constant value 10 for the parameter ex:intParameterA.

Example 19: 
ex:add10 a fnoc:PartiallyAppliedFunction;
    fnoc:partiallyApplies ex:sumFunction ;
    fnoc:parameterBinding [
      fnoc:boundToTerm 10 ;
      fnoc:boundParameter ex:inParameterA
    ] .

This is equivalent to the following function/composition:

Example 20: 
ex:add10 a fno:Function ;
    fno:name            "add10"^^xsd:string ;
    dcterms:description "This function adds 10 to its integer parameter."^^xsd:string ;
    fno:expects ( ex:intParameterB ) ;
    fno:returns ( ex:sumOutput ) .

ex:add10Composition a  fnoc:Composition ;
    fnoc:composedOf [
        fnoc:mapFromTerm 10 ;
        fnoc:mapTo [
            fnoc:constituentFunction ex:sumFunction ;
            fnoc:functionParameter ex:intParameterA 
        ] 
    ],
    [
        fnoc:mapFrom [
            fnoc:constituentFunction ex:add10 ;
            fnoc:functionParameter ex:intParameterB
        ] ;
        fnoc:mapTo [
            fnoc:constituentFunction ex:sumFunction ;
            fnoc:functionParameter ex:intParameterB 
        ]
    ], 
    [
        fnoc:mapFrom [
            fnoc:constituentFunction ex:sumFunction ;
            fnoc:functionOutput ex:sumOutput 
        ];
        fnoc:mapTo [
            fnoc:constituentFunction ex:add10 ;
            fnoc:functionOutput ex:sumOutput
        ]
    ] .

4.4.1 fnoc:PartiallyAppliedFunction

A function derived from another function by providing one or more, but not all parameter values.

4.4.1.1 fnoc:partiallyApplies

Domain fno:PartiallyAppliedFunction

Range fno:Function

Expresses that the function in the subject is a partial application of the object function. It is expected that the partial application provides a constant value for at least one of the function's parameters. If no parameter values are specified the use of fnoc:partiallyApplies is equivalent to fnoc:applies.

4.4.1.2 fnoc:ParameterBinding

Represents parameter bindings in partial function applications, combining some value (any RDF term), via fnoc:boundToTerm and one of the function's parameters, via fnoc:boundParameter.

4.4.1.3 fnoc:parameterBinding

Domain fno:PartiallyAppliedFunction

Range fnoc:ParameterBinding

4.4.1.4 fnoc:boundToTerm

Domain fnoc:ParameterBinding

4.4.1.5 fnoc:boundParameter

Domain fnoc:ParameterBinding

Range fno:Parameter

5. Examples

The following sections are a set of FAQs and How-to's regarding the Function Ontology.

5.1 Array of parameters

The model allows for arrays of parameters. For example, the following function function findInString(str, [searchValues...]): boolean could be described as follows:

Example 21: 
# Function description
ex:findInString a fno:Function ; 
    fno:name "Finding multiple values in a string function"^^xsd:string ; 
    dcterms:description "This function returns true if any of the input values is found in the string."^^xsd:string ;
    fno:expects (
        [ fno:predicate ex:body; fno:required "true"^^xsd:boolean ]
        [ fno:predicate ex:searchValues; fno:required "true"^^xsd:boolean ]
    ) ;
    fno:returns (
        [ fno:predicate ex:found; fno:required "true"^^xsd:boolean ]
    ) .

# Execution description
ex:findExecution a fno:Execution ;
    fno:executes ex:findInString ;
    ex:body "Try and find some values in this string."^^xsd:string ;
    ex:searchValues ("Paris" "Brussels" "Tokyo" "Los Angeles") .

# After execution, following triple is created
ex:findExecution ex:found "false" .

5.2 Required output

Output can be assigned required or not. For example, thrown errors are an example of optional output.

6. Relation to other types of descriptions

6.1 Web services

There exist many specifications that define Web services, both non-semantically (e.g., WSDL [wsdl] and WADL [wadl]) and semantically (e.g., OWL-S [owls] and Hydra [hydra]) These specifications target different facets (e.g., HTTP-based vs SOAP-based access, defining RESTful APIs, etc.), but have in common that they define Web services. Thus, they clearly specify, e.g., which HTTP method to invoke with which parameter to correctly call the Web service. The big drawback of these specifications is thus that they are very coupled with the technology stack. However, not all actions can be executed using Web APIs, either because of performance or practicality reasons.

A. References

A.1 Normative references

[hydra]
Hydra Core Vocabulary. W3C. 08 December 2020. Unofficial Draft. URL: https://www.hydra-cg.com/spec/latest/core/
[owls]
OWL-S: Semantic Markup for Web Services. W3C. 22 November 2004. W3C Member Submission. URL: https://www.w3.org/Submission/OWL-S/
[rdf-primer]
RDF Primer. Frank Manola; Eric Miller. W3C. 10 February 2004. W3C Recommendation. URL: https://www.w3.org/TR/rdf-primer/
[RFC2119]
Key words for use in RFCs to Indicate Requirement Levels. S. Bradner. IETF. March 1997. Best Current Practice. URL: https://www.rfc-editor.org/rfc/rfc2119
[RFC8174]
Ambiguity of Uppercase vs Lowercase in RFC 2119 Key Words. B. Leiba. IETF. May 2017. Best Current Practice. URL: https://www.rfc-editor.org/rfc/rfc8174
[skos-primer]
SKOS Simple Knowledge Organization System Primer. Antoine Isaac; Ed Summers. W3C. 18 August 2009. W3C Working Group Note. URL: https://www.w3.org/TR/skos-primer/
[wadl]
Web Application Description Language. W3C. 31 August 2009. W3C Member Submission. URL: https://www.w3.org/Submission/wadl/
[wsdl]
Web Service Definition Language (WSDL). W3C. 15 March 2001. W3C Working Group Note. URL: https://www.w3.org/TR/wsdl

A.2 Informative references

[10.1016/j.future.2019.10.006]
Implementation-independent function reuse. Ben De Meester; Tom Seymoens; Anastasia Dimou; Ruben Verborgh. Elsevier. September 2020. Future Generation Computer Systems. URL: https://doi.org/10.1016/j.future.2019.10.006