The Function Ontology

1. Conformance

As well as sections marked as non-normative, all authoring guidelines, diagrams, examples, and notes in this specification are non-normative. Everything else in this specification is normative.

The key words MUST and SHOULD in this document are to be interpreted as described in BCP 14 [RFC2119] [RFC8174] when, and only when, they appear in all capitals, as shown here.

2. The Problem

Functions are processes that perform a specific task by associating one or more inputs to an output. They are essential building blocks of information retrieval and information management, and of computer science in general. For example, during extraction of birthdates from a semi-structured dataset, normalization of these dates improves further analysis.

However, the development, maintenance, and support efforts of implementing these functions are fragmented. Efforts are fragmented across different development contexts (i.e., a combination of, among others, programming language, programming paradigm, and architecture), and it is not feasible to consolidate these efforts by limiting all developers to the same development context. On the one hand because implementations are tuned to meet different requirements, on the other hand due to prior investment. Thus, the same function can have multiple implementations, each within a specific development context. For example, a function to normalize dates may have implementations available as a piece of JavaScript source code, as part of a JAVA software package, and within a RESTful Web service.

This specification (and accompanying ontology) explains how to semantically declare and describe functions, their input parameters, and possible outputs. Instead of defining technology-specifics, the functions are described independent of the technology that implements them. By semantically defining these functions using an ontology, we provide a uniform and unambiguous solution, and thus, we can close the gap between semantic data and any real-world action, and enable semantic applications to be used in real-world scenarios.

We furthermore provide links to other – not further specified – concepts such as problems and algorithms, and specify the additional mappings of these abstract functions to (existing) concrete implementations.

3. Definitions

The following document makes a clear distinction between following concepts:

• A function declaration is stating that a function exists, without further ado. For example, function sum is a function declaration.
• A function description describes the function, i.e., talks about the inputs and outputs of the function. For example, the function above can have the following description: function int sum(int a, int b), namely, the function sum has two input parameters, int a and int b, and returns an integer.
• An assignment fills in the values of the parameters of a functions. For example, a possible assignment for the exemplary function could be sum(2, 4), namely, assigning the values 2 to a and 4 to b.

Furthermore, we define following concepts:

• A function is a process that performs a specific task. In essence, its identification is a function declaration. A function can associate one or more parameters to an output. A function can have input parameters, output, solve certain problems, and can be implemented using certain algorithms. It's execution can also be described in an implementation-independent manner, see https://fno.io/spec/#dfn-execution. The ontology term is defined at fno:Function.
• A problem is a general issue. Some problems can be solved by executing a certain function. For example, the above function solves the doing a sum problem, however, "global warming" could also be perceived as a problem, with no single function to solve it. The ontology term is defined at fno:Problem.
• An algorithm is a specified set of instructions, independent of its implementation (e.g., Dijkstra's shortest path algorithm). A function can be implemented using a known algorithm, or use a combination of multiple algorithms to solve a certain problem. A function does not have to be implemented by any algorithm or have to be mapped one-on-one to an algorithm. It is not required to have a one-to-one mapping between an algorithm and a problem. The ontology term is defined at fno:Algorithm.
• A parameter is the description of the input value of a function. For example, the above function has two parameters, a and b. The ontology term is defined at fno:Parameter.
• An output is the description of the output value of a function. For example, the above function has one output, an integer. A function can have multiple outputs (e.g., callbacks in JavaScript can return multiple results, or a function could throw multiple types of errors). A function with all parameters and outputs defined is a function description. The ontology term is defined at fno:Output.
• An execution is the assignment of the values of the parameters of a function. An execution has as result the value of the output of the function. For example, sum(2, 4) is an execution of the example function. The value of the output is known after the function is executed, and should in this case be the integer 6. The ontology term is defined at fno:Execution.
• An implementation defines the internal workings of one or more functions. This depends on the used development context, i.e., the used programming language and execution environment. An implementation could be, e.g., an NPM package. The ontology term is defined at fno:Implementation.
• A mapping links (abstract) functions and (concrete) implementations. The ontology term is defined at fno:Mapping.

In this specification, a problem and algorithm are not described in further detail. We mostly provide generic relations to point to other vocabularies or ontologies. This way, problems and algorithms can be further specified in complementary vocabularies.

4. The Function Ontology

The Function Ontology distinguishes between the (abstract) function and the (concrete) implementation. The two can be used together, but are complementary.

4.1 Function (abstract)

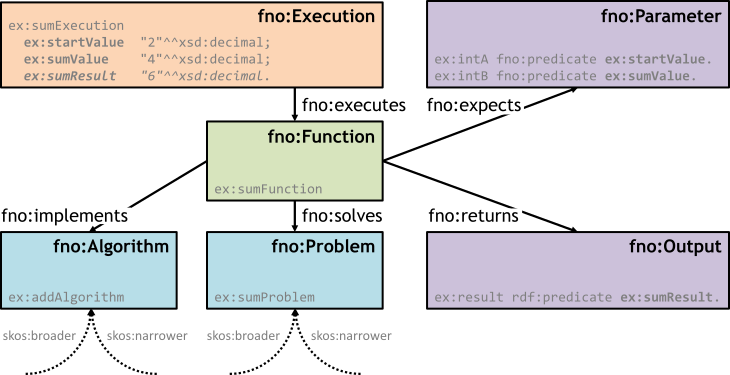
The Function Ontology follows the Content Ontology Design Pattern and consists of a couple of base classes that need to be instantiated for real world use cases. Input parameters and output values are connected to functions via executions, using a reification paradigm [rdf-primer].

It uses SKOS to define relations between functions, problems, and algorithms [skos-primer].

To be consistent with the paradigms used in SKOS, axioms need to be made instead of subclassing the base classes of the Function Ontology. The reification paradigm allows to define the connection between an execution and the input parameters and output values. This allows for reusing these connection definitions, and more meaningful connections between input parameters and execution.

No cardinalities are defined in the Function Ontology, as there are no hard limits on cardinality to be defined. A function can implement multiple algorithms, solve multiple problems, and have multiple executions. All executions can have multiple input parameters and output values. Vice versa, input parameters and output values can be linked to multiple executions, and an execution (i.e., a set of input values and output values) can be linked to multiple functions.

4.1.1 fno:Function

Example 1:

ex:sumFunction
    a                   fno:Function ;
    fno:name            "The sum function"^^xsd:string ;
    dcterms:description "This function can do the sum of two integers."^^xsd:string .

This is a function declaration: a sum function is defined and described.

4.1.2 fno:Problem

Example 2:

ex:sumFunction
    a          fno:Function ;
    fno:solves ex:sumProblem .

ex:sumProblem
    a                   fno:Problem ;
    fno:name            "The sum problem"^^xsd:string ;
    dcterms:description "This handles the problem of adding two integers to each other."^^xsd:string ;
    skos:broader        ex:mathProblem .

Functions can be linked to Problems, which are more general descriptions than functions, e.g., the “Euclidean distance”-function is related to the “Distance”-problem. To create a more specific organization, problems can be further interlinked with each other using the SKOS standard [skos-primer].

Note

skos terms can be used to relate problems with each other. This can also be done for algorithms and functions.

4.1.2.1 fno:solves

Domain fno:Function

Range fno:Problem

4.1.3 fno:Algorithm

Example 3:

ex:sumFunction
    a              fno:Function ;
    fno:implements ex:sumAlgorithm .

ex:sumAlgorithm
    a                   fno:Algorithm ;
    fno:name            "The sum algorithm"^^xsd:string ;
    dcterms:description "About how to add two integers to each other."^^xsd:string ;

4.1.3.1 fno:implements

Domain fno:Function

Range fno:Algorithm

4.1.4 fno:Parameter

Example 4:

ex:sumFunction
    a           fno:Function ;
    fno:expects ( ex:intParameterA ex:intParameterB ) .

ex:intParameterA
    a             fno:Parameter ;
    fno:predicate ex:startValue ;
    fno:type:     xsd:integer ;
    fno:required  "true"^^xsd:
        boolean .

ex:intParameterB
    a             fno:Parameter ;
    fno:predicate ex:sumValue ;
    fno:type:     xsd:integer ;
    fno:required  "true"^^xsd:boolean .

A Function expects a list of Parameters and returns a list of Outputs. This description actually defines which predicates to use when binding the values to the execution of the function. The parameters are ordered in a list, and each parameter defines the relationship that is used for the execution. For this, the fno:predicate predicate MUST be used. All predicates are allowed, except for rdf:type and fno:executes. A Parameter can have a specific type or other metadata (e.g., required or not, having a default value or not).

To specify the datatype of the parameter, the fno:type predicate SHOULD be used.

To specify whether a parameter is required, the fno:required predicate SHOULD be used.

In the example ex:intParameterA and ex:intParameterB can be reused across function descriptions. As they only describe the parameters, and not the actual values, they can be reused. For example, the function function match(str, regex) and function split(str, regex) could reuse the same parameter instantiations.

The fno:expects predicate has as range rdf:List. This could be used to hint applications how many parameters are used, and in what order, however, this is not enforced. This to accommodate technologies where the order of parameters is not important.

4.1.4.1 fno:expects

Domain fno:Function

Range rdf:List of fno:Parameter

4.1.4.2 fno:predicate

Domain fno:Function

Range rdf:Property

4.1.4.3 fno:type

Domain fno:Parameter

4.1.4.4 fno:required

Domain fno:Parameter

Range xsd:boolean

4.1.5 fno:Execution

Example 5:

ex:sumExecution
    a             fno:Execution ;
    fno:executes  ex:sumFunction ;
    ex:startValue "2"^^xsd:integer ;
    ex:sumValue   "4"^^xsd:integer.

The Execution shows how the predicates are used as described as Parameters of the Function. rdf:type and fno:executes cannot be used as parameter predicates, as this would conflict with the description of the execution.

4.1.5.1 fno:executes

Domain fno:Execution

Range fno:Function

4.1.6 fno:Output

Example 6:

ex:sumFunction
    a           fno:Function ;
    fno:returns ( ex:sumOutput ) .

ex:sumOutput
    a             fno:Output ;
    fno:predicate ex:sumResult ;
    fno:type:     xsd:integer ;
    fno:required  "true"^^xsd:boolean .

A function's output is also a list, as multiple values can be returned (e.g., a Web API can return a body and a status code, a local implementation can return a value or throw an error). Similar as with fno:Parameter, the connecting predicate is described for fno:Output. To specify the datatype of the output, similarly, the fno:type predicate SHOULD be used.

After the execution of the function with the correct parameter values, we could return the following turtle:

Example 7:

ex:sumExecution
    a            fno:Execution ;
    ex:sumResult "6"^^xsd:integer.

Similarly as with the parameter descriptions, the output descriptions can be reused across functions.

4.1.6.1 fno:returns

Domain fno:Execution

Range fno:Output

4.1.7 Complete example

Declaration and description of the function and one execution:

Example 8:

ex:sumFunction
    a                   fno:Function ;
    fno:name            "The sum function"^^xsd:string ;
    dcterms:description "This function can do the sum of two integers."^^xsd:string ;
    fno:solves          ex:sumProblem ;
    fno:implements      ex:sumAlgorithm ;
    fno:expects         ( ex: intParameterA ex:intParameterB ) ;
        fno:returns ( ex:sumOutput ) .

ex:intParameterA
    a             fno:Parameter ;
    fno:predicate ex:startValue ;
    fno:type:     xsd:integer ;
    fno:required  "true"^^xsd:boolean .

ex:intParameterB
    a             fno:Parameter ;
    fno:predicate ex:sumValue ;
    fno:type:     xsd:integer ;
    fno:required  "true"^^xsd:boolean .

ex:sumOutput
    a             fno:Output ;
    fno:predicate ex:sumResult ;
    fno:type:     xsd:integer ;
    fno:required  "true"^^xsd:boolean .

ex:sumProblem
    a                   fno:Problem ;
    fno:name            "The sum problem"^^xsd:string ;
    dcterms:description "This handles the problem of adding two integers to each other."^^xsd:string ;
    skos:broader        ex:mathProblem .

ex:sumAlgorithm
    a                   fno:Algorithm ;
    fno:name            "The sum algorithm"^^xsd:string ;
    dcterms:description "About how to add two integers to each other."^^xsd:string .

ex:sumExecution
    a             fno:Execution ;
    fno:executes  ex:sumFunction ;
    ex:startValue "2"^^xsd:integer ;
    ex:sumValue   "4"^^xsd:integer .

Resulting output triples:

Example 9:

ex:sumExecution
    a            fno:Execution ;
    ex:sumResult "6"^^xsd:integer .

4.2 Implementation (concrete)

4.2.1 fno:Implementation

Example 10:

ex:leftPadImplementation
    a         fnoi:NpmPackage ;
    doap:name "left-pad" .

4.2.1.1 Example: Hydra

Link with the Hydra specification.

The Hydra specification defines Web services semantically. A hydra:ApiDocumentation can thus be seen as a specific fno:Implementation.

4.2.2 fno:Mapping

A fno:Mapping maps a fno:Function to a (part) of an fno:Implementation. For example: a left-pad function is mapped to a specific method in an NPM package. This requires the combination of 3 types of mappings:

• the mapping of the method name (so that, e.g., a ex:leftPad function is mapped to method doLeftPadding()),
• the mapping of the parameters (so that, e.g., the argument with predicate ex:inputString of the function is mapped to the second parameter of the doLeftPadding() method), and
• the mapping of the outputs (so that, e.g., both the return value and the thrown exception of the method are mapping to the outputs of the function).

To link to the function and implementation, predicates fno:function and fno:implementation are used, respectively.

Note that the actual implementations and mappings are not part of the Function Ontology. Specific development contexts can be further catered to.

Example 11:

ex:leftPadMapping
    a                  fno:Mapping ;
    fno:function       ex:leftPad ;
    fno:implementation ex:leftPadImplementation .

4.2.2.1 fno:MethodMapping

Maps the method name. For source code, this can be done using a fnom:StringMethodMapping. The method name is an attribute of a fnom:StringMethodMapping, linked using the fnom:method-name predicate.

Example 12:

ex:leftPadMapping
    a                 fno:Mapping ;
    fno:methodMapping [ a                fnom:StringMethodMapping ;
                        fnom:method-name "doLeftPadding" ] .

4.2.2.2 fno:ParameterMapping

Maps the different parameters. For source code, this is typically specified by the position, using fnom:PositionParameterMapping: each fno:ParameterMapping gets linked to a parameter using the fnom:functionParameter predicate, and to a position using the fnom:implementationParameterPosition predicate.

Example 13:

ex:leftPadMapping
    a                    fno:Mapping ;
    fno:parameterMapping [ a                                    fnom:PositionParameterMapping ;
                           fnom:functionParameter               ex:inputStringParameter ;
                           fnom:implementationParameterPosition "2"^^xsd:int ] .

For a Web service, this is typically specified by a name, e.g., a POST using property "password" in the form body. A fnom:PropertyParameterMapping is used. Each fno:ParameterMapping gets linked to a parameter using the fnom:functionParameter predicate, and to a property using the fnom:implementationProperty predicate.

4.2.2.3 fno:ReturnMapping

Maps the different outputs. For source code, this is typically specified by the return value, and (optionally) thrown exceptions, using fnom:DefaultReturnMapping and fnom:ExceptionReturnMapping, respectively: each fno:ReturnMapping gets linked to an output using the fnom:functionOutput predicate.

Example 14:

ex:leftPadMapping
    a                 fno:Mapping ;
    fno:returnMapping [ a                   fnom:DefaultReturnMapping ;
                        fnom:functionOutput ex:outputStringOutput ] .

4.2.3 Execution with a Mapping

4.2.3.1 fno:uses

The metadata of the mapping can be linked to the execution using the fno:uses predicate

Example 15:

ex:leftPadExecution
    fno:uses ex:leftPadMapping

ex:leftPad
    a           fno:Function ;
    fno:expects ( ex:inputStringParameter ex:paddingParameter ) ;
    fno:returns ( ex:outputStringOutput ) .

ex:inputStringParameter
    a             fno:Parameter ;
    fno:predicate ex:inputString ;
    fno:type      xsd:string ;
    fno:required  "true"^^xsd:boolean .

ex:paddingParameter
    a             fno:Parameter ;
    fno:predicate ex:padding ;
    fno:type      xsd:int ;
    fno:required  "false"^^xsd:boolean .

ex:leftPadImplementation
    a         fnoi:NpmPackage ;
    doap:name "left-pad" .

ex:leftPadMapping
    a                    fno:Mapping ;
    fno:function         ex:leftPad ;
    fno:implementation   ex:leftPadImplementation ;
    fno:methodMapping    [ a                fnom:StringMethodMapping ;
                           fnom:method-name "doLeftPadding" ] ;
    fno:parameterMapping [ a                                    fnom:PositionParameterMapping ;
                           fnom:functionParameter               ex:inputStringParameter ;
                           fnom:implementationParameterPosition "2"^^xsd:int ] ;
    fno:parameterMapping [ a                                    fnom:PositionParameterMapping ;
                           fnom:functionParameter               ex:paddingParameter ;
                           fnom:implementationParameterPosition "1"^^xsd:int ] ;
    fno:returnMapping    [ a                   fnom:DefaultReturnMapping ;
                           fnom:functionOutput ex:outputStringOutput ] .

5. Examples

The following sections are a set of FAQs and How-to's regarding the Function Ontology.

ex:findInString a fno:Function ; 
    fno:name "Finding multiple values in a string function"^^xsd:string ; 
    dcterms:description "This function returns true if any of the input values is found in the string."^^xsd:string ;
    fno:expects (
        [ fno:predicate ex:body; fno:required "true"^^xsd:boolean ]
        [ fno:predicate ex:searchValues; fno:required "true"^^xsd:boolean ]
        [ fno:predicate ex:found; fno:required "true"^^xsd:boolean ]
    ) .

ex:findExecution a fno:Execution ;
    fno:executes ex:findInString ;
    ex:body "Try and find some values in this string."^^xsd:string ;
    ex:searchValues ("Paris" "Brussels" "Tokyo" "Los Angeles") .

6. Relation to other types of descriptions